
For the “Alberology” column (or better “treeology”, from the Italian “alberologia”), I had the pleasure of exploring with forester Antonio De Bona the link that unites trees, and nature more generally, to a discipline that is apparently somewhat difficult and, perhaps, most often considered useless and boring but, in my opinion, extremely fascinating, precisely because of its rigour and complexity: mathematics.
Since its origins, it has been considered the science par excellence, the ‘science of sciences’: indeed, every scientific or technical discipline (from physics to engineering, from economics to computer science) makes extensive use of the analysis, calculation and modelling tools it offers.
As early as the 19th century, the French philosopher and founder of Positivism, Auguste Comte, considered it to be the fundamental science that enabled all other disciplines to achieve the ‘positive state’. The oldest evidence of mathematical knowledge is, however, much older (2500-3000 BC) and is found in some pre-Hellenic civilisations in the Middle East. In Egyptian papyri and Babylonian tablets, calculations, determinations of areas and volumes, and first- and second-degree problem solving have been found, testifying to the fact that these peoples were already using arithmetic and geometry for practical activities such as trade, cadastral surveying (land surveying), navigation and agriculture.
Over the centuries, the concept of ‘pure’ mathematics (which studies mathematical problems without taking into account their possible practical use) has evolved and changed with the aim of finding suitable solutions to concrete problems, through the development of tools and models useful for the purposes of sciences such as physics, chemistry and biology.
In the early years of the 20th century, in particular, applications of mathematics to biology began to take hold, thanks to the work of mathematicians Vito Volterra and Alfred J. Lotka on interacting populations, which was followed by work by other mathematicians on population genetics, the spread of epidemics, development, neurobiology…
Despite an initial scepticism on the part of some biologists about the actual ability of mathematics to simplify and describe biological systems, biomathematics (also known as mathematical biology) has undergone a strong acceleration since the 1960s as a result of a growing interest in the discipline, which has opened the way for new areas of research.
Going back in time, we actually discover that mathematics has been used in biology as far back as the 13th century, when the Italian mathematician Leonardo da Pisa, better known as Fibonacci, in order to study the descent of a pair of rabbits devised a succession of integers, called the Golden (or Fibonacci) Succession, in which each element is equal to the sum of the two preceding ones: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…
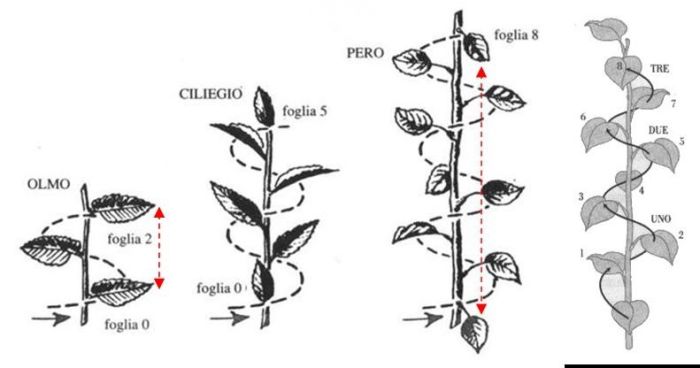
Fibonacci also noticed that the ratio between one number in the sequence and the one immediately preceding it was getting closer and closer to the irrational number Φ (Phi) = 1.618…, the so-called ‘golden number’, also called the Golden Section or Phidian Constant. This ratio is very recurrent in nature and can be found in the form of a logarithmic spiral (called a ‘golden spiral’ because it repeats the proportions of the Golden Section ad infinitum) when observing the geometry of plants, flowers and fruits, in the shells of molluscs or even in the hives of bees. The Fibonacci succession, in particular, plays a fundamental role in phyllotaxis, which is precisely the branch of botany that studies the order in which the organs (leaves, branches, flowers or seeds) of a plant species are arranged, based on the repetition of regular patterns.
Kepler discovered that on many types of trees the leaves are aligned according to a pattern involving two Fibonacci numbers: starting from any one leaf, after one, two, three or five turns from the spiral you will always find a leaf aligned with the first and, depending on the species, this will be the second, third, fifth, eighth or thirteenth.
The concepts of pattern and symmetry are widespread in nature. If we think of trees, the left-right symmetry that recurs in children’s drawings immediately comes to mind, but also the root-branch symmetry found in the more elaborate drawings of adults. Observing trunks and branches in cross-section, we can note another type of symmetry, the radial symmetry, which presupposes the existence of a main axis through which several planes of symmetry pass, dividing the object (in this case the trunk or branches) into many equal and symmetrical parts.

The Pythagorean tree is an example, on the other hand, of a structure with bilateral symmetry (i.e. with a single plane of symmetry that divides the object into two equal, perfectly symmetrical parts) that recalls the appearance of a real tree, but is nothing more than a mathematical fractal: a square has one side in common with an isosceles right triangle, which in turn has the other two sides in common with two other squares, and so on. The sum of the areas of the two smallest squares, by Pythagoras’ theorem, is equal to the area of the initial square, and so also the areas of the squares that are formed in subsequent steps, added together, will give the area of the first square. By constructing any right-angled triangle on the side of the first square, one can have an asymmetrical tree whose wrapped shape is nothing more than a logarithmic spiral.
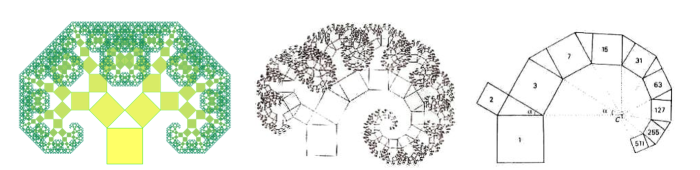
Fractals are geometric figures endowed with internal homotety, i.e. self-similar (enlarging any of their parts produces a figure similar to the original) that repeat themselves ad infinitum. From the snowflake to the peacock’s tail, nature is full of fractal elements: just think, for example, of the Roman broccoli, in which the number of rosettes that compose it is always a number of the Fibonacci succession, or the fern, in which each single component of the leaf is similar to the complete leaf and each component is, in turn, made up of sub-components (small leaves) similar to the single component and the complete leaf.
500 years ago, Leonardo Da Vinci had realised that trees are also fractal in nature: by observing their branches, he noticed that the primary branches were repeated in similar, smaller structures, the secondary branches. In his notebook he wrote that “all the branches of a tree at every stage of its height, when put together, have a thickness equal to the trunk”: in other words, if the branches of a tree were bent upwards and pressed together, the tree would look like a large trunk with the same thickness from top to bottom.
Da Vinci’s tree theory was explored by French physicist Christophe Eloy in a study published in 2011 in Physical Review Letters, one of the most prestigious physics journals. Eloy conducted a series of simulations to demonstrate that the tree skeleton has a self-similar structure and that the diameters of the branches are adapted to resist wind-induced stress with minimal biomass. In the end, the physicist’s simulations confirmed Da Vinci’s rule and thus the structural theory of trees that would explain their ability to withstand stresses; however, some scientists and researchers lean more towards the hydrological theory, according to which, instead, trees would have their own characteristic shape because this would favour a more efficient transport of sap.

Although there is still little experimental data to support Da Vinci’s observations, his theory still continues to fascinate and inspire scientists, researchers and artists around the world after centuries and leaves the door open to further research that could reveal new and exciting discoveries about forest structure and tree evolution.
Today, by means of mathematics, we are able to know how tall a tree is, estimate its volume (woody biomass) in m³ and its growth rate (increment) over time, and consequently estimate the economic value of an entire stand. In particular, thanks to financial mathematics operations, which allow us to transfer monetary values over time, we are able to calculate the interest that accrues over the years on the initial capital (woody capital).
The agrarian economics expert Arrigo Serpieri noted in this regard how in forest production “the costs gradually advanced are fixed for a long time in the growing plants”; Duerr, in his Fundamentals of forest economics, defines wood capital as a “machine” that produces wood, itself destined to become a product at the moment of felling (“wood is produced from wood”). It is easy, therefore, to consider woody capital as an anticipation of capital, where one considers forest production on a periodic basis, or as standing trees (part of the land capital) where one has a view of forest production on an annual basis, as in the case of a settled forest, endowed with a growing stock (woody capital) constant over time.
By studying the widths of the growth rings (dendrochronology) of an individual plant and their anomalies, we are also able to reconstruct the past history of the entire forest and thus the favourable, unfavourable and even events such as landslides and floods.
Mathematics, therefore, through a series of more or less complex formulas and laws, helps us to better understand the balances and mechanisms on which nature is based and to look at it with new eyes, allowing us to admire its infinite beauty and, no less, its extreme fragility.
“Mathematics can be seen as that which unites and interposes itself between Man and Nature, between the external world and the internal world, between thought and perception.”
F. W. August Fröbel






































